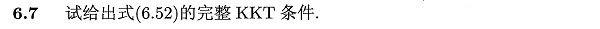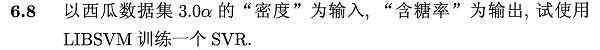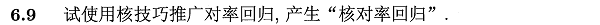本章学习了支持向量机。基础知识部分包括SVC、软间隔、核技巧、SVR等,实践部分涉及了SVM、SVR的实现。
查看相关答案和源代码,欢迎访问我的Github:PnYuan/Machine-Learning_ZhouZhihua.
本章概要
本章讲述支持向量机(Support Vector Machine,SVM),相关内容包括:
- 支持向量分类器(SVM classifier)
支持向量(support vector)、间隔(margin)、最大间隔(maximum margin)、支持向量机(SVM)、对偶问题(dual problem)、拉格朗日乘子法;
- 核技巧(kernel trick)
特征空间映射、高维可分、内积(inner product)、核函数(kernel function)、核矩阵(kernel matrix)半正定性、再生希尔伯特空间(RHKS)、核函数选择、多项式核、高斯核、Sigmoid核;
- 软间隔(soft margin)
硬间隔、软间隔、松弛变量(slack variables)、替代损失函数(surrogate loss function)、
- 支持向量回归(SVR)
支持向量机的优劣总结
支持向量机模型的好处很多,这里不做赘述,下面列出些在使用支持向量机方法时,需要注意的问题:
- SVM涉及到求解二次规划,在大规模数据的训练时会产生很大的开销,为此常会引入一些高效算法来应对,如采用SMO(sequential minimal optimization)来加速二次优化问题求解;
课后练习
6.1 公式推导

6.2 不同核函数对应的支持向量差别分析
本题的详细内容见:
周志华《机器学习》课后习题解答系列(七):Ch6.2 - 支持向量分析实验
6.3 SVM与BP网络、C4.5决策树等的对比实验
本题的详细内容见:
周志华《机器学习》课后习题解答系列(七):Ch6.3 - SVM对比实验
6.4 线性核SVM与LDA的关联
SVM与LDA均可用于样本最优划分超平面的求解,即法向向量 ω ,参考文献Comparing Linear Discriminant Analysis and Support Vector Machines中对LDA与SVM的本质描述,一般有:
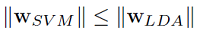
考虑到线性核SVM的输入空间与特征空间相同,那么取等的条件是:
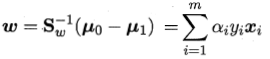
这说明两者生成的超平面相同,此时等效。
6.5 高斯核SVM与RBF网络的关联
两种方法均采用径向基函数(RBF)如下:
- SVM的超平面表示为:
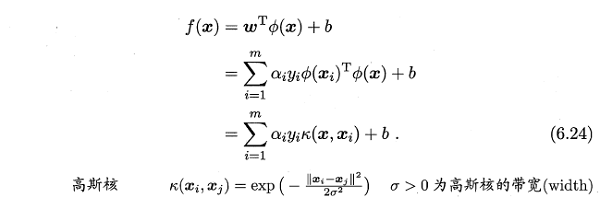
- RBF网络表示为:
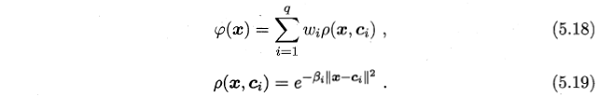
可以看出两者的表达式颇为相似,进一步分析,假设采用RBF网络作为一个二分类器,参考文献Comparing Support Vector Machines with Gaussian Kernels to Radial Function Classiers,两者分类函数对比如下:
- SVM的分类器表示为:
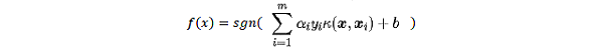
- RBF网络分类器表示为:
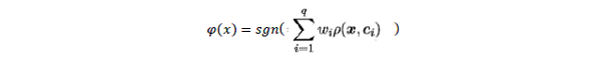
对于两个分类器,SVM的表达式多出了偏置项,同时其系数项 ω 只与支持向量有关;RBF网络的系数项 ω 与由输入样本训练得到,但是对于非支持向量对应的样本,其 ω数值相对非常小。
6.6 SVM对噪声的敏感分析
SVM的决策边界(超平面)是由支持向量所确定的,即是利用相对较少的数据特征来学得整个数据的特性。由于支持向量相对较少,其上的噪声会对超平面的确定产生相对较大的影响。
6.7 KKT条件推导
参考书中附录公式B.3,KKT条件即拉格朗日函数在对参数进行偏导取0计算后,为求得最优解,乘子和约束必须满足其中之一为0的条件。
要获取式(6.52)的完整KKT条件,只需将式(6.47~6.50)代入该式即可。
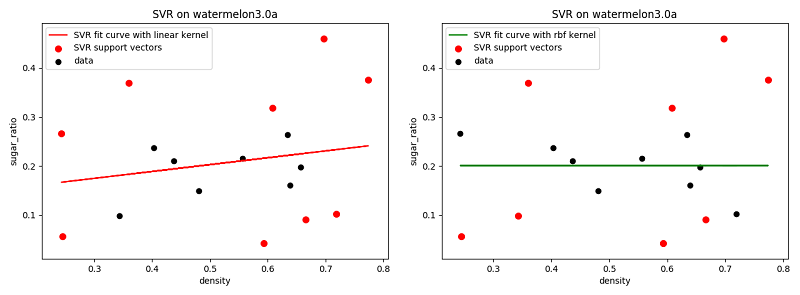
6.8 SVR实验
基于python-sklearn工具包,在线性核和高斯核下的SVR拟合如下图示:
可以看出,由于数据自变量与因变量间关系随机性较强,采用SVR拟合效果不佳;
6.9 核对率回归模型设计
关于核对率回归(KLR),可参考书p132中关于 log 损失函数下SVM与LR的比较,也可参考台大林轩田-机器学习技法中关于KLR的slide。
简要说明如下:
6.10 SVM改进设计
支持向量的规模与SVM计算速度息息相关,在不影响模型性能的情况下减少支持向量数目,能有效提高SVM效率。为此,一些稀松算法如 1-norm SVM, Lp-SVM, 自适应Lp-SVM 被提出,给出两篇参考文献如下: