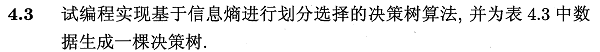本章讲述决策树的相关内容,包括决策树的生成、剪枝、连续值、缺失值的处理、多变量决策树等内容。
所涉及的编程练习答案和源代码托管在Github:PnYuan/Machine-Learning_ZhouZhihua,欢迎访问.
本章概要
本章讲述决策树(decision tree),相关内容包括:
- 决策树生成(construction)
子决策(sub-decision)、递归生成算法(basic algorithm)、最优划分属性、纯度(purity)、信息熵(information entropy)、信息增益(information gain)、ID3 、增益率(gain ratio)、C4.5 、基尼指数(gini index)、CART;
- 剪枝(pruning)
过拟合、泛化能力、预剪枝(prepruning)(自上而下)、决策树桩(decision stump)、欠拟合、后剪枝(postpruning)(自下而上)、完全树。
- 连续属性、缺失值(continuous variables, missing values)
连续属性离散化、二分法(bi-partition)、值缺失时属性划分、缺值样本划分、权重、加权信息增益;
- 多变量决策树(multivariate decision tree)
斜划分、斜决策树(oblique decision tree)、非叶节点-线性分类器;
此外还提及了C4.5Rule、OC1、感知机树等拓展方法,以及增量学习算法ID4、ID5R、ITI等;
决策树的优劣总结
参考sklearn官网 - 1.10.Decision Trees总结如下:
优势(Advantages):
- 易理解,解释性好,易可视化;
- 数据预处理少;
- 复杂度O(logN);
- 支持标称变量+连续变量;
- 支持多输出;
- 白盒模型,布尔逻辑;
- 模型好坏易验证;
- 容忍先验知识错;
劣势(Disadvantages):
- 决策树生成易太大、过拟合;(需要剪枝、设置树最大深度等后续操作。)
- 模型生成不稳定,易受小错误样本影响;
- 学习最优模型是N-P难题,贪心搜索易陷入局部最优;(可采用随机初始化生成多个模型。)
- 不支持非线性逻辑,如XOR;
- 数据不平衡时生成的树形差;
课后练习
4.1.冲突数据影响决策树
考虑决策树的生成(书p74图4.2),算法生成叶节点,并递归返回条件有:
- 当前节点的所有样本属于同一类,叶节点类标签 -> 当前类;
- 当前节点的所有样本在属性上取值相同,叶节点类标签 -> 样本中最多类;
由此可见,若两训练数据样本特征向量相同,那么它们会到达决策树的同一叶节点(只代表某一类),若二者数据标签不同(冲突数据),则会出现训练误差,决策树与训练集不一致。
如果没有冲突数据,到达某节点的样本会出现以下两种情况:
- 样本间特征向量相同且属于同一类,满足递归结束条件,该节点为叶节点,类标签正确(无训练误差);
- 样本间特征向量不同时,递归结束条件不满足,数据会根据属性继续划分,直到上一条情况出现。
综上得证,当数据集不含冲突数据时,必存在与训练集一致(训练误差为0)的决策树。
4.2.决策树划分选择准则
由于训练集和真实集往往存在差异,若采用训练误差作为度量,模型常会出现过拟合,导致泛化能力差。
4.3.编程实现ID3算法
即ID3算法,这里我们基于Python独立编程实现。详细过程见:
周志华《机器学习》习题解答:Ch4.3 - 编程实现ID3算法
4.4.编程实现CART算法与剪枝操作
即CART算法,这里我们基于Python独立编程实现。详细过程见:
周志华《机器学习》习题解答:Ch4.4 - 编程实现CART算法与剪枝
4.5.基于对率回归进行划分选择
这里提一下我的思路:
参考书p90-91的多变量决策树模型,这里我们将每个非叶节点作为一个对率回归分类器,输出为”是”、”否”两类,形成形如二叉树的决策树。
4.6.各种决策树算法的比较
简要的分析一下:
- ID3算法基于信息熵增益,CART算法则采用了基尼系数。两种划分属性选择均是基于数据纯度的角度,方法差距应该不大(CART可能要好一点)。而对率回归进行划分选择,以斜划分的方式,实现了多变量参与划分,其模型决策边界更光滑。
- 相比于决策树的生成算法,剪枝操作更影响模型性能。
4.7.非递归决策树生成算法 - DFS
下面主要是本题的一种视角:
首先做一些分析:
- 从数据结构算法的角度来看,生成一棵树常用递归和迭代两种模式。
- 采用递归时,由于在递归时要存储程序入口出口指针和大量临时变量等,会涉及到不断的压栈与出栈,当递归层次加深,压栈多于出栈,内存消耗扩大。
- 这里要采用队列数据结构来生成决策树,虽然避免了递归操作产生的内存消耗,但需要更大的额外存储空间。
- 用MaxDepth来控制树的深度,即深度优先(Depth Fisrt)的形式,一般来说,使用递归实现相对容易,当然也可以用非递归来实现。
下面设计出基于队列+深度控制的决策树非递归生成算法:
----
输入: 训练集 D = {(x1,y1),(x2,y2),...,(xm,ym)}.
属性集 A = {a1, a2,...,ad}.
过程: 函数 TreeGenerate(D,A):
1. 生成根节点 root;
2. 初始化深度 depth = 0;
3. 生成栈 stack (为保存顶节点root及其对应的数据D和深度depth);
4.
5. while D != Φ OR stack不为空:
6. if D != Φ, then
7. if D中样本全属于同一类别C, then
8. root标记为C类叶节点, D = Φ, continue;
9. end if
10. if depth == MaxDepth OR D中样本在属性A上取值相同, then
11. root标记为D取值中最多类的叶节点, D = Φ, continue;
12. end if
13. 从A中选择最优划分属性a*, 令Dv表示D中在a*上取值为a*v的样本子集;
14. 生成子节点 child, 为root建立分支指向child;
15. 将[root, D\{Dv}, A, depth]压入栈stack;
16. 令 root = child, D = Dv, A = A\{a*}, depth = depth+1;
17. else
18. 从stack中弹出[root, D, A, depth];
19. end if
输出: 树的根节点root.(即以root为根节点的树)
----
实际上,这里的算法实用的是栈而非完全意义上的队列。
个人认为,从数据结构的角度来看,栈和队列的最大区别在于FILO和FIFO,即存取元素时索引的区别,并不存在太大的存储实现区别。进一步说明,对于很多程序环境,如C++,Java等,均可以基于队列(Queue)构造栈(Stack)结构,由此构建的栈数据结构和队列底数据结构层实现相同。
题干中所说的栈“溢出”,主要应该是指递归时程序信息压栈所导致,相比于非递归的算法,其压栈数据量大得多。
故而此处的算法实现直接采用栈实现。
关于本题的另一种视角是:
对于深度优先搜索,采用队列存储每层当前节点的兄弟节点与父节点,这样队列的消耗相较于上面的一种方法要大一些(如当前节点的兄弟节点,父节点及其兄弟节点,祖父节点及其兄弟节点…)。
4.8.非递归决策树生成算法 - BFS
本题实际上是BFS与DFS的比较:
- 对于深度优先搜索,每深入一层需要存储上一层节点的信息以方便回溯遍历(其存储的是一条路径);
- 对于广度优先搜索,每深入一层需要存储当前层兄弟节点信息以实现遍历(其存储的是每层信息,存储量会大一些但);
两种方法各自有防止队列过大化的阈值(即MaxDepth和MaxNode),所以两种方法均可将内存消耗控制在一定范围之内。
当数据属性相对较多,属性不同取值相对较少时,树会比较宽,此时深度优先所需内存较小,反之宽度优先较小。