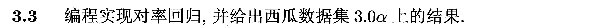本章讲述线性模型,涉及线性回归、对率回归、线性判别分析、多分类、类别不平衡等内容。并包含编程实验。
本章概要
本章开始涉及编程练习,相关答案和源代码托管在我的Github上:PnYuan/Machine-Learning_ZhouZhihua.
本章讲述线性模型(linear model),相关内容包括:
- 线性回归(linear regression)
序关系(order)、均方差(square error)最小化、欧式距离(Euclidean distance)、最小二乘法(least square method)、参数估计(parameter estimation)、多元线性回归(multivariate linear regression)、广义线性回归(generalized linear model)、对数线性回归(log-linear regression);
- 对数几率回归(逻辑回归)(logistic regression)
分类、Sigmoid函数、对数几率(log odds / logit)、极大似然法(maximum likelihood method);
- 线性判别分析(linear discriminant analysis - LDA)
类内散度(within-class scatter)、类间散度(between-class scatter);
- 多分类学习(multi-classifier)
拆解法,一对一(One vs One - OvO)、一对其余(OvR)、多对多(MvM)、纠错输出码(ECOC)、编码矩阵(coding matrix)、二元码、多标记学习(multi-label learning);
- 类别不平衡(class-imbalance)
再缩放(rescaling)、欠采样(undersampling)、过采样(oversampling)、阈值移动(threshold-moving);
习题解答
3.1.线性回归模型偏置项
偏置项b在数值上代表了自变量取0时,因变量的取值;
1.当讨论变量x对结果y的影响,不用考虑b;
2.可以用变量归一化(max-min或z-score)来消除偏置。
3.2.证明对数似然函数是凸函数(参数存在最优解)
直接给出证明结果如下图:
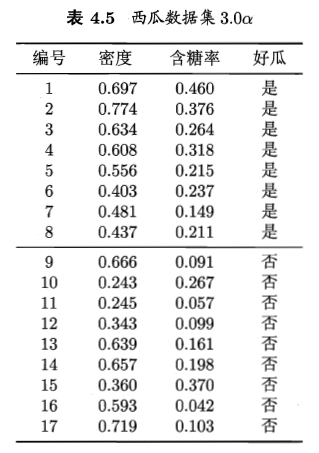
3.3.编程实现对率回归
所使用的数据集如下:
本题是本书的第一个编程练习,采用了自己编程实现和调用sklearn库函数两种不同的方式(查看完整代码):
具体的实现过程见:周志华《机器学习》习题解答:Ch3.3 - 编程实现对率回归
3.4.比较k折交叉验证法与留一法
本题采用UCI中的iris data set 和 Blood Transfusion Service Center Data Set 数据集,借助sklearn实现(查看完整代码)。
具体的实现过程见:周志华《机器学习》习题解答:Ch3.4 - 交叉验证法练习
3.5.编程实现线性判别分析
本题采用题3.3的西瓜数据集,采用基于sklearn实现和自己独立编程实现两种方式(查看完整代码)。
具体的实现过程见:周志华《机器学习》习题解答:Ch3.5 - 编程实现线性判别分析
3.6.线性判别分析的非线性拓展思考
给出两种思路:
- 参考书p57,采用广义线性模型,如 y-> ln(y)。
- 参考书p137,采用核方法将非线性特征空间隐式映射到线性空间,得到KLDA(核线性判别分析)。
3.7.最优ECOC编码方式
参考书p65,对于同等长度的编码,理论上来说,任意两个类别间的编码距离越远,纠错能力越强。那么如何实现呢,可参考文献Error-Correcting Output Codes。下图是截取文中的关于在较少类时采用exhaustive codes来生成最优ECOC二元码的过程:
采用文中方法,每两类的Hamming Distance均达到了码长的一半,这也是最优的编码方式之一。
3.9.多分类到二分类分解、类别不平衡
参考书p66,对OvR、MvM来说,由于对每类进行了相同的处理,其拆解出的二分类任务中类别不平衡的影响会相互抵销,因此通常不需专门处理。
以OvR(一对其余)为例,由于其每次以一个类为正其余为反(参考书p63),共训练出N个分类器,在这一过程中,类别不平衡由O的遍历而抵消掉。